n1cef1sh's Blog
前言
对于密码学实在是很头大,没有足够的数学功力支撑,有时候理解和实践起来要慢很多。这里简单记录一下关于Feistel cipher的知识。
简介
Feistel cipher是一种用于构造分组密码的对称结构,大部分分组密码使用该方案,包括DES(数据加密标准)。它的优点在于加密机密操作非常相似,某些情况下甚至是相同的,只需要逆转密钥编排。因此,实现这种密码所需的代码或电路大小能几乎减半。
构造细节
首先简单概括一下:
- 1、给明文分组(L,R)
- 2、对R进行加密
- 3、密文 = 加密后的R + L(LR位置交换)
详细的来说:
- 加密的方式——轮函数F,每轮有不同的K作为密钥
- 对于第i轮来说(i<=n,i是下标,格式原因没做出下标效果)
- L(i+1) = Ri
- R(i+1) = Li ⊕ F(Ri,K(i+1))
- 假设加密16轮(比如DES)R’L’表示密文的一部分
- 那么(L16,R16) = (R’0,L’0)
- 最后置换得到的密文L’0,R’0
解密则为其逆过程,要点即轮函数的密钥要倒着使用Kn,Kn-1,……,K1。
- 先将密文分组L,R。
- 对于第i轮来说:
- L(i+1) = Ri
- R(i+1) = Li ⊕ F(Ri,Kn-i-1)
- 循环直到(L’16,R’16) = (R0,L0)
- 置换得到明文L0R0
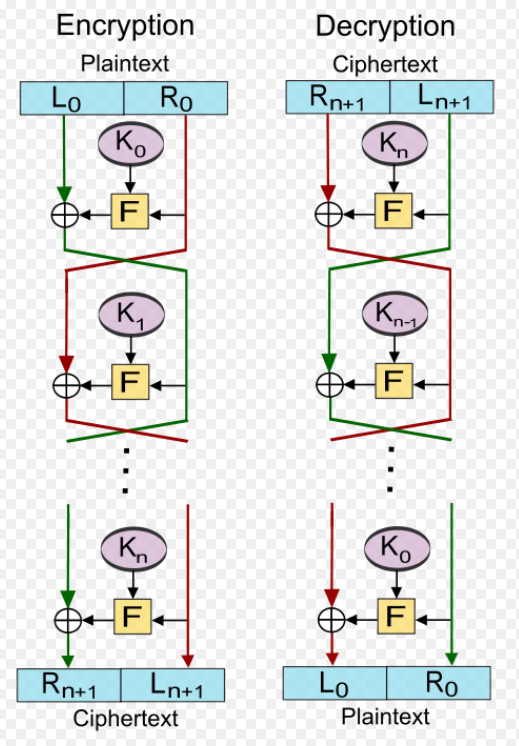
构造原理如下图(图片来自维基)
影响参数
Feistel结构的具体实现依赖于以下参数和特征:
-
分组长度:分组长度越长意味着安全性越高,但是会降低加、解密的速度。这种安全性的增加来自更好的扩散性。传统上,64位的分组长度比较合理,在分组密码设计里很常用。
-
密钥长度:密钥较长同样意味着安全性较高,但会降低加、解密的速度。这种安全性的增加来自更好的抗穷尽攻击能力和更好的混淆性。现在一般认为64位的密钥还不够。通常使用的密钥长度是128位。
-
迭代轮数:Feistel密码的本质在于单轮不能提供足够的安全性而多轮加密可取得很高的安全性。迭代轮数的典型值是16。
-
子密钥产生算法:子密钥产生越复杂,密码分析就越困难。
-
轮函数F:同样,轮函数越复杂,抗攻击的能力就越强。
护网杯初赛crypto——fez
fez.py
import os
def xor(a,b):
assert len(a)==len(b)
c=""
for i in range(len(a)):
c+=chr(ord(a[i])^ord(b[i]))
return c
def f(x,k):
return xor(xor(x,k),7)
def round(M,K):
L=M[0:27]
R=M[27:54]
new_l=R
new_r=xor(xor(R,L),K)
return new_l+new_r
def fez(m,K):
for i in K:
m=round(m,i)
return m
K=[]
for i in range(7):
K.append(os.urandom(27))
m=open("flag","rb").read()
assert len(m)<54
m+=os.urandom(54-len(m))
test=os.urandom(54)
print test.encode("hex")
print fez(test,K).encode("hex")
print fez(m,K).encode("hex")
fez.log
048d26224aae9f6be49f13202c0b173c2346909fcbba868d5d9b7431002957c5c01c546530f84e45b8a3892526401c007bca7d39b0b7
69d41820c61c7e8fb47fde8f09064f24af72dc6251e97e72bdc2d7c0b4696110ef84f30da6ac88b7059500f8e814cec9e9e13bcafad8
32e7094533a1e76ac8acdeb882c0d6965ca954d75dfd00e759b5aff9663f41d49ae70ee18fd3c067ad7ae577433ad2512b764f4b2eb2
分析题目可知是个基础的feistel结构,加密的轮函数F只是一个XOR异或操作,且只加密了7轮。最后给了三个输出,分别是测试值/测试值加密后/flag加密后。
我们不知道每一轮的密钥Kn,但是可以通过前两个值得出K,然后将加密后的FLAG倒推即可。附一个根据TMCTF的wp修改的脚本,需要注意的是最后根据轮数不同,结果会稍有差别,这里把三种情况都列出来了。
from crypto_commons.generic import long_to_bytes
n = 216 #p_str长度的一半
#如果p_str c_str s_str长度不同的话,把短的那个前面补0,转二进制时可能会长度不同
#三个str依次对应test/Etest/Eflag的二进制
p_str = '011011000011010001010010010110111100110010001100000000000100101010111011101100101000000101010000001100010101010000101000010010011101101011101010110111100100111101110111010001000010010110100110101001001001111001010100010100011000100011110110011100001100111001000110011001111101111110011101101100001011011111011110110100101010001001011100110110101010011011100010101000100110111100001101001110000100110110010110100110011001100010001111'
c_str = '100011001111100001111100110000111100010101010011011010010010010101011011000111000000110111010100001110000100000010010010000000100110101011101010000111100011011110001001100101100111010111011110100011001101001110100000100101111111000000001010000101001010011101110010111111110001001101010010010000001111110100000011111001110111110010011101101000000010110101111010001010111100010110010000111111100111100101111100111111101110100110010000'
#print (len(p_str))
p_m0 = int(p_str[:n], 2)
p_m1 = int(p_str[n:], 2)
p = [p_m0, p_m1]
c_m0 = int(c_str[:n], 2)
c_m1 = int(c_str[n:], 2)
s_str = '111011000100001010111001100001110110101001110001011000111001001110101000110100010111011101101011011111100100101111101000010001010001000101010001000110111010010101111001010000000100111101011001100101010110110011100110111111010001001011111100011011001011111110111010100100001001110001101110010110100110101010110011111001110100011010101110110001011101001100011101110001100010111001001000000000000000100100110001011110101111000110111011'
s_m0 = int(s_str[:n], 2)
s_m1 = int(s_str[n:], 2)
def decrypt(m0, m1):
k0 = c_m0
for e in m0:
k0 ^= p[e]
k1 = c_m1
for e in m1:
k1 ^= p[e]
d_m0 = s_m0^k0
d_m1 = s_m1^k1
if len(m0) == 2:
d_m0 ^= d_m1
if len(m1) == 2:
d_m1 ^= d_m0
print(long_to_bytes(d_m0), long_to_bytes(d_m1))
#加密循环轮数不同结果会稍有差别
decrypt([0,1],[0])
decrypt([0],[1])
decrypt([1],[0,1])
#flag{festel_weak_666_lol9991234admin}
三种情况的解释:
secret_0 = flag_1 ^ final_key0
secret_1 = flag_0 ^ flag_1 ^ final_key^1
secret_0 = flag_0 ^ final_key0
secret_1 = flag_1 ^ final_key^1
secret_0 = flag_0 ^ flag_1 ^ final_key0
secret_1 = flag_0 ^ final_key^1
参考资料
https://zh.wikipedia.org/wiki/%E8%B4%B9%E6%96%AF%E5%A6%A5%E5%AF%86%E7%A0%81
https://www.tonlyshy.cn/article/av11
https://github.com/pberba/ctf-solutions/tree/master/20180915_trendmicro/forensics_crypto_1_400